Suma y promedio de los valores mayores de una lista.

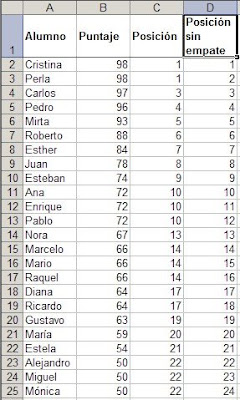
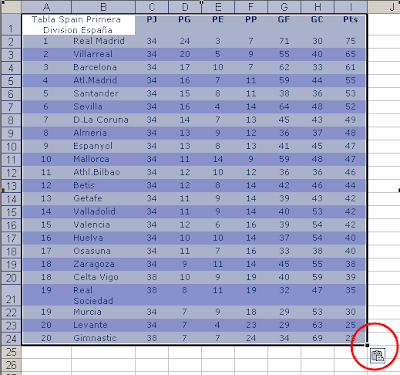
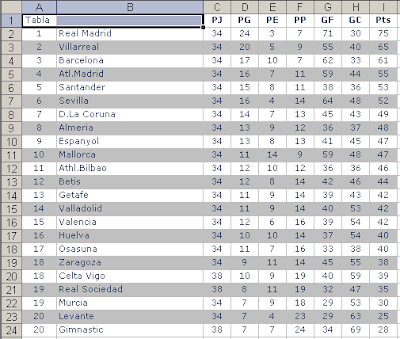
Supongamos esta lista de personas (Pedro, Rubén y Marcos) con valores arbitrarios para los meses de enero hasta octubre

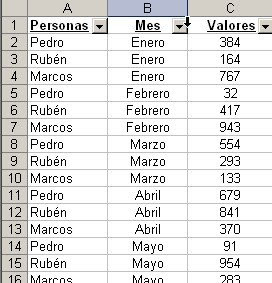
Definimos dos nombres, uno que contiene el rango A2:A31 (Personas) y otro que contiene el rango C2:C30 (Valores)



Ahora podemos calcular con facilidad el total y el promedio de los valores para cada una de las personas

La función para SUMA es

=SUMAR.SI(personas;$E2;valores)

y para PROMEDIO

=SUMAPRODUCTO((personas=E2)*valores)/CONTAR.SI(personas;E2)

Para el promedio también pueden usar esta fórmula matricial:

={PROMEDIO(SI(((personas=E2)*valores)<>0;valores;FALSO))}

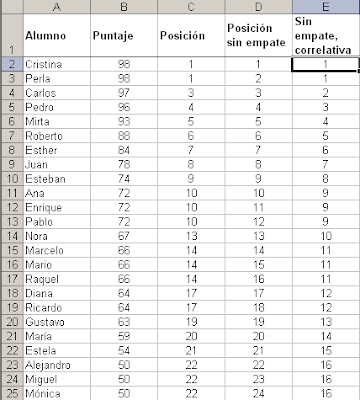
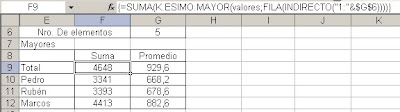
Un lector me consultaba hace unos días como calcular la suma (o el promedio) de los cinco mayores valores de cada persona.

Para esta tarea usamos esta fórmula matricial, que a continuación explicaré


={SUMA(K.ESIMO.MAYOR(((personas=$E10)*valores);FILA(INDIRECTO("1:"&$G$6))))}

La clave de esta fórmula es la función K.ESIMO.MAYOR. Esta función tiene dos argumentos: una lista de valores y el número de orden del valor que queremos obtener. Al usar esta función en una fórmula matricial obtenemos una matriz de valores de acuerdo al criterio que fijamos con la función.
La expresión (personas=$E10)*valores) genera una matriz con los valores del rango "valores" que corresponden a Pedro o cero si corresponde a un nombre distinto.
Para indicar que queremos, por ejemplo, los cinco valores mayores, tenemos que poner como segundo argumento de K.ESIMO.MAYOR una matriz como {1,2,3,4,5}. En lugar de esto usamos FILA con INDIRECTO, poniendo en la celda G6 la cota superior de nuestra matriz. En nuestro ejemplo

FILA(INDIRECTO("1:"&$G$6))

dentro de a fórmula matricial genera la matriz {1,2,3,4,5}. La ventaja de este método es que con cambiar el valor en G6, cambiamos la cantidad de elementos a ser tenidos en cuenta, sin necesidad de reescribir la fórmula.

Si queremos hacer las operaciones para los cinco menores valores de cada persona, por ejemplo, tenemos que complicar un poco nuestra fórmula (que ya dista de ser sencilla!)

={SUMA(K.ESIMO.MENOR(SI((personas=$E17)*valores<>0;(personas=$E17)*valores;FALSO);FILA(INDIRECTO("1:"&$G$6))))}



En esta fórmula tenemos que agregar la función SI para eliminar los ceros que aparecen en la matriz (personas=$E17)*valores
En la fórmula para calcular los valores mayores estos ceros no "molestan" ya que de por si son los menores. Pero cuando queremos calcular los valores menores de cada persona, tenemos que eliminarlos.
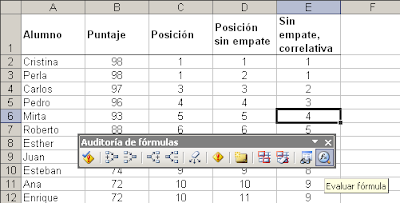
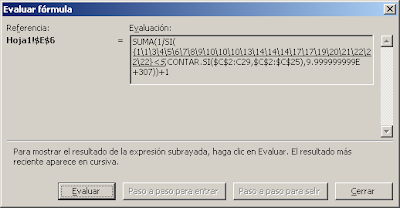
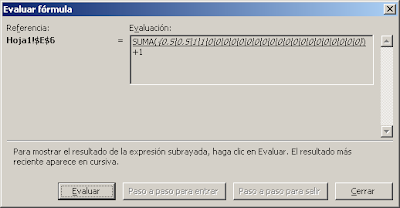
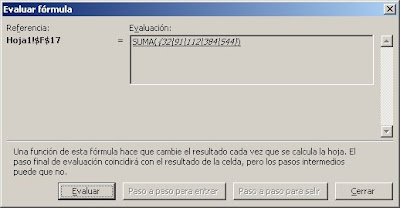
Para ver este problema más claramente podemos usar el botón Evaluar de la barra de herramientas Auditoría de fórmulas



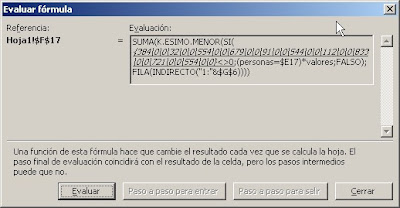
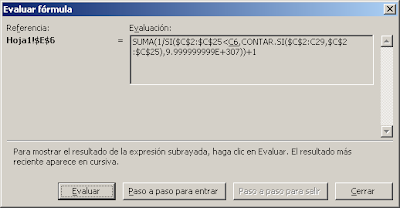
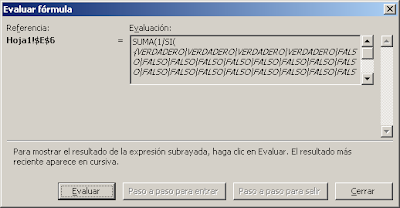
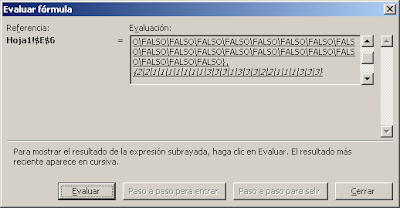
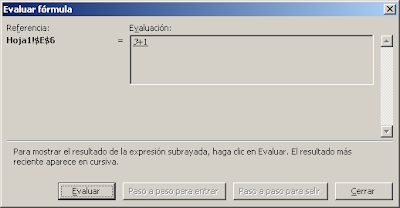
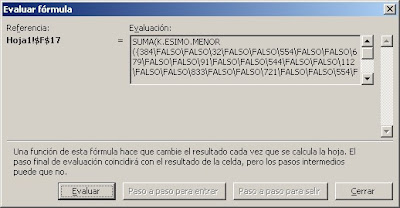
Como ven la matriz generada contiene ceros en los valores que no corresponden al criterio elegido ("Pedro" en nuestro ejemplo). Al usar la función SI

SI((personas=$E17)*valores<>0;(personas=$E17)*valores;FALSO)

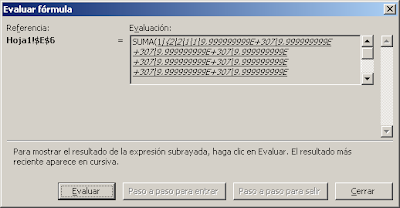
dentro de la fórmula matricial, obtenemos FALSO en lugar de ceros




Esto nos permite calcular correctamente nuestra suma y promedio para los valores menores del rango.



El cuaderno con el ejemplo se puede descargar aquí.

Buen fin de semana y mis disculpas por la demora en responder a las muchas consultas que llegan a mi mail. Lamentablemente algunas de ellas quedarán sin responder.

Technorati Tags: MS Excel

Como determinar fechas de iniciación o fin de tareas con Excel

Cálculos de fechas es una de los temas sobre los cuales recibo muchas consultas. He tratado el tema en varias notas. Si pulsan el enlace Fechas y Hora podrán acceder a todas la notas sobre el tema en el blog.

Uno de los cálculos más triviales es determinar la fecha de conclusión de una tarea sabiendo la fecha de inicio y la cantidad de días requeridos. Esto se hace con una simple operación de suma. Si ponemos en la celda B1 la fecha de inicio (03/01/2008) y en la celda B2 los días requeridos para completar la tarea (35), en la celda B3 ponemos =B1+B2




Si queremos hacer el cálculo tomando en cuento sólo los días hábiles, tenemos que usar la función DIA.LAB (WORKDAY en la versión inglesa). Esta función está disponible sólo si hemos instalado el complemento Analysis Toolpak



Como pueden ver, la tarea será concluida en 49 días, dentro los cuales hay 7 sábados y 7 domingos.


Un lector me consultaba como hacer la cuenta a la inversa. Es decir, dados los días requeridos y la fecha de cierre, cuando debemos comenzar nuestra tarea?

En el caso de tratarse de días corridos (sin tomar en cuenta los feriados), sencillamente restamos los días requeridos de la fecha de cierra



Si queremos hacer el cálculo sólo con días hábiles, la solución también es sencilla, pero no tan intuitiva. Usamos DIA.LAB, donde el primer argumento es la fecha de cierre y el segundo los días hábiles requeridos pero expresados como número negativo



Nótese el signo "-" delante de B17.

Como habrán notado, esta función tiene un tercer argumento, opcional, que permite introducir una lista de días festivos.

Technorati Tags: MS Excel

Gráficos de Barra en lugar de columnas

De toda la colección de gráficos que ofrece Excel, tal vez el de columnas sea el más usado. Si bien el gráficos de barras parece ser un gráfico de columnas volteado 90 grados, hay situaciones en las cuales su uso me parece más recomendable.
En mi blog sobre gráficos y presentación de datos puede leer una nota sobre por qué prefiero este gráfico de barras, a pesar del trabajo extra que requiere construirlo



a éste de columnas que Excel construye con solo dos clics del mouse

Technorati Tags: MS Excel

Ordenando rangos por jerarquía con Excel – Reseña

La función JERARQUIA de Excel calcula la posición relativa de un valor dentro de una lista. En notas anteriores hemos mostrado como usar esta función, sus limitaciones y algunas formas de superarlas.
En la nota Construir con Excel una tabla con las 10 primeras posiciones mostramos como superar el problema el "empate". Allí dimos el ejemplo de esta lista de calificaciones de alumnos



En la columna C usamos la función JERARQUIA para determinar la posición de cada alumno de acuerdo a la calificación. Allí vemos que Perla y Cristina, que tienen la misma calificación, obtienen el mismo número de rango (1) y Carlos recibe el número 3. Para solucionar esta situación usamos la función JERARQUIA combinada con CONTAR.SI para "desempatar" entre alumnos con la misma calificación. La fórmula en la columna D es

=JERARQUIA(B2,puntaje)+CONTAR.SI($B$2:B2,B2)-1


Un lector me pregunta como hacer para que el alumno Carlos, que tiene la segunda mejor nota, aparezca con el número 2 ya que ocupa el segundo lugar y no con el número tres. Es decir, que cada alumno aparezca con el numero de posición que ocupa.
Para lograr esto tendremos que usar una fórmula desarrollada por Tushar Mehta. En nuestra tabla hemos agregado la columna D, que muestra el resultado deseado



La fórmula en la columna D es

={SUMA(1/SI($C$2:$C$25<C2,CONTAR.SI($C$2:C25,$C$2:$C$25),9.999999999E+307))+1}

Esta es una fórmula matricial. . Primero la introducimos la fórmula en la celda D2 pulsando CTRL+MAYUSCULAS +ENTER simultáneamente. Luego la copiamos al esto del rango (hasta D25 e nuestro ejemplo).
Algunos detalles a tomar en cuenta en esta fórmula:

# - La fórmula usa la columna C como columna auxiliar. Esta columna contiene la posición de cada alumno calculada con la función JERARQUIA.

# - La expresión CONTAR.SI($C$2:C25,$C$2:$C$25) calcula cuantas veces aparece un determinado valor en el rango, sólo si no se trata de la primera posición. Para determinar si el valor evaluado no es el de la primera posición, usamos la expresión $C$2:$C$25<C4.

# - La segunda parte la función SI, 9.999999999E+307 es un número expresado en forma exponencial y es el mayor número que Excel puede aceptar. Esto es necesario para evitar la división por cero cuando evaluamos el valor del primer puesto. La operación 1/9.999999999E+307 da como resultado 0.

Para ver como funciona esta fórmula, lo mejor es usar el botón Evaluar de la barra de auditoría de fórmulas.



Por ejemplo, seleccionamos la celda D5 y apretamos el botón Evaluar fórmula



Apretamos el botón Evaluar del diálogo y vemos la expresión que va a ser evaluada



Al volver a apretar Evaluar vemos el resultado de la operación



En nuestro caso, se genera una matriz con 4 resultados VERDADERO y el resto FALSO.
En el próximo paso, Evaluar nos muestra la matriz generada por CONTAR.SI



Ahora vemos que el resultado de CONTAR.SI es la matriz {2,2,1,1,1,9,99..9E+07…}



Al dividir los miembros de esta matriz por 1 obtenemos



Y al sumar la nueva matriz, nos da



Es decir, 4, la posición del valor en la lista.

Technorati Tags: MS Excel

Importar datos WEB a Excel – otras alternativas

En una nota anterior mostramos como importar datos de tablas que se encuentran en la Internet a Excel.
Las ventajas y los beneficios de usar este método son obvios, en especial si tomamos en cuenta que cada día más y más información se encuentra en tablas de la Internet.
En la nota mencionada vimos como crear una consulta Internet en Excel con el menú Datos-Obtener datos externos-Nueva consulta WEB.
Si trabajan con Explorer (versión 5.0 en adelante), existen otros métodos de crear estas consultas:

Usar Copiar y Pegar.
Abrimos una página de Internet con la tabla que queremos importar. Por ejemplo, esta tabla de posiciones de la liga española




Seleccionamos la tabla con el Mouse, tal como seleccionaríamos un rango en una hoja de Excel, la copiamos (Ctrl+C) y la pegamos a la hoja de destino.
En el ángulo inferior derecho de la tabla que acabamos de pegar veremos el icono de Opciones de pegado



Abrimos el menú y elegimos la opción Crear consulta WEB actualizable



Excel abre el diálogo de Nueva consulta WEB, donde elegimos la tabla que queremos importar (caso contrario, importará elementos que tal vez no queremos)



También podemos abrir el menú Opciones y elegir el tipo de formato que queremos obtener



Finalmente apretamos Importar

Como ven tendremos que aplicar algunos formatos, ya que el resultado no es del todo estético (la falta de "ñ" se debe a que he cambiado el computador y todavía no he redefinido los idiomas)



Después de aplicar los formatos (los fondos grises los hacemos con la técnica de formato condicional que ya hemos mostrado),



cambiamos algunas definiciones en el cuadro de Propiedades de la barra de Datos Externos para evitar que sean modificados al actualizar la consulta



Editar desde el Explorer
Abrimos la página y en el menú Archivo del Explorer, elegimos la opción Editar con Excel



Esto abrirá el diálogo de Nueva consulta WEB. A partir de aquí todo el proceso es como en el caso anterior.
Si en el Explorer aparece Word como opción de edición, pueden cambiar a Excel usando el menú de Opciones del Explorer y cambiando al opción de editor de HTML a Excel

Technorati Tags: MS Excel

Calcular depreciación con Excel – Segunda nota

En la primer nota del tema vimos las distintas funciones que Excel pone a nuestra disposición para calcular la depreciación de un bien.
En esta nota veremos cómo construir una tabla, o cédula, de depreciación para todos los bienes de una empresa imaginaria. Esta tabla debe asistirnos en el cálculo de total del monto de depreciación que será reconocido como gasto en el cuadro de ganancias y pérdidas de la empresa del período.
Nuestro modelo, que calcula la depreciación de los bienes sobre una base mensual usando el método lineal, es el siguiente




La celda B1 contiene la fecha en base a la cual queremos calcular la depreciación. Aquí ponemos el último día del mes en cuestión. El modelo calcula el total de la depreciación a reconocer para el mes en la celda B2. Esta celda contiene la fórmula =SUMA(Depreciación_del_período)

Donde "Depreciación_del_período" es el nombre que contiene el rango dinámico

=DESREF('con auxiliares'!$F$5,0,0,CONTARA('con auxiliares'!$F:$F)-1,1)

Esto nos permite que el total tome en cuenta los bienes que vayamos agregando en la tabla.

Los campos Descripción, Fecha de adquisición, % de depreciación anual y valor residual son los datos de nuestro modelo. Hay que prestar atención que el porcentaje de depreciación es introducido en términos anuales, pero los cálculos serán realizados por mes.

Para realizar los cálculos podemos adoptar dos técnicas: con o sin tablas auxiliares. En esta nota mostraremos las dos soluciones, pero sin entrar a considerar cuál es el método más apropiado.

Dado que usamos el método lineal, calculamos la depreciación del período (mes) con la función SLN. Para calcular los períodos transcurridos desde la adquisición de los bienes, usaremos la función SIFECHA.
Aquí tenemos que tomar en cuenta que existe la posibilidad de que uno o más bienes hayan sido depreciados (amortizados) completamente. Para evaluar esta posibilidad creamos una tabla auxiliar



En la columna J (Total de meses) usamos la fórmula =1/D5*12. Esto nos da el total de meses de vida útil del bien.

En la columna K (Transcurridos) usamos la fórmula =SIFECHA(B5,$B$1,"m"), que calcula la cantidad de meses transcurridos desde la adquisición del bien, incluido el mes del cálculo.

La columna L (Restantes) nos da la diferencia entre J y K. Este resultado será nuestro indicador si el bien debe ser depreciado o no. En caso de ser negativo, el bien ha sido depreciado en su totalidad.

Una vez construida la tabla auxiliar, ponemos las fórmulas en para nuestros cálculos:

Depreciación del período (F): =SI(L5>0,SLN(C5,E5,1/D5*12),0)

Depreciación acumulada (G): =SI(L5>0,SIFECHA(B5,$B$1,"m")*F5,C5-E5)

Saldo (H): obviamente =C5-G5

Si queremos construir nuestro modelo sin tablas auxiliares, lo que hacemos es crear fórmulas que incluyas las auxiliares. En la hoja "sin auxiliares" del archivo con el ejemplo pueden ver la aplicación de estas fórmulas

Depreciación del período (F): =SI((1/D5*12-SIFECHA(B5,$B$1,"m"))>0,SLN(C5,E5,1/D5*12),0)

Depreciación acumulada (G): =SI((1/D5*12-SIFECHA(B5,$B$1,"m"))>0,SIFECHA(B5,$B$1,"m")*F5,C5-E5)



Un punto a tomar en cuenta es que hacemos los cálculos por meses enteros. Es decir, la antigüedad de un bien es la misma sin importar en que día del mes haya sido adquirido.
En algunos sistemas se considera el primer mes como completo sólo si el bien ha sido adquirido (o puesto en marcha) antes del día 15 del mes.
En la hoja "con auxiliares (2)" hemos modificado la fórmula de la columna K (Transcurridos) de manera que la cuenta de meses se haga de acuerdo a esta regla:

=SI(DIA(B5)<15,SIFECHA(B5,$B$1,"m"),SIFECHA(B5,$B$1,"m")-1)

Otro punto a tomar en cuenta es que si la fecha en B1 es anterior a la fecha de adquisición de un bien, las fórmulas que se refieren a el darán un resultado #NUM!. Esta situación podría darse si queremos calcular el total de la depreciación en un período del pasado.
En este modelo he optado por el uso de Formato condicional para volver "invisible" el contenido de las celdas que dan un resultado de error




También tenemos que modificar la fórmula en la celda B2, para obtener el total sin errores. Para esto usaremos la técnica mostrada en la nota sobre operaciones con rangos que contienen errores. En nuestro caso ponemos esta fórmula matricial

={SUMA(SI(ESERROR(Depreciación_del_período),0,Depreciación_del_período))}



Todo esto se puede ver en la hoja "con auxiliares (3)" del cuaderno con el ejemplo.



Technorati Tags: MS Excel

Calcular depreciación con Excel – Primera nota

Una de las consultas que recibo con cierta frecuencia es como construir una tabla de depreciación de bienes con Excel.
.
Empecemos por definir que depreciación, que en algunos países de habla castellana se llama también amortización. Depreciación es la pérdida de valor de un bien a lo largo del tiempo. Del punto de vista económico, la depreciación expresa la reducción de la vida útil económica del bien. Del punto de vista contable, la depreciación es la asignación del costo del bien al período contable en que ha sido usado.
De acuerdo a los países y a las prácticas contables, la depreciación es calculada de distinta manera. Excel nos provee con funciones para calcular la depreciación de acuerdo a los métodos más aceptados:

SLN: calcula la depreciación por método directo de un bien en un período dado. La sintaxis es

SLN(costo;valor_residual;vida)

SYD: calcula la depreciación por suma de dígitos de los años de un bien durante un período específico. La sintaxis es

SYD(costo;valor_residual;vida;período)

DB: calcula la depreciación de un bien durante un período específico usando el método de depreciación de saldo fijo. La sintaxis es

DB(costo;valor_residual;vida;período;mes)

DDB: calcula la depreciación de un bien en un período específico con el método de depreciación por doble disminución de saldo u otro método que se especifique. La sintaxis es

DDB(costo,valor_residual,vida,período,factor)


Con estas funciones podemos construir una tabla de depreciación (o amortización) de un bien. Demos un ejemplo para comparar los distintos métodos, que serán calculados con las funciones de Excel. Supongamos estos datos

En este ejemplo hemos supuesto un valor residual de 1, y la depreciación está calculada en términos de años. Naturalmente, la depreciación puede calcularse en términos de meses o cualquier otra unidad de tiempo y el valor residual puede ser cualquier número positivo.

Esta tabla nos muestra los resultados de los distintos métodos (he omitido el método DDB)



Al representar gráficamente los resultados, podemos apreciar claramente las diferencias entre los distintos métodos



El archivo con el ejemplo se puede descargar aquí.

En la próxima nota veremos cómo construir un pequeño modelo para manejar la depreciación de los bienes de una empresa imaginaria.


Technorati Tags: MS Excel