Determinar la última fecha de un acontecimiento.

Un ejemplo similar, y tal vez más práctico, del problema de determinar la posición de un elemento en un vector es la consulta que me dirige un lector de México.
Dada una lista de clientes y fechas de contacto, queremos determinar cuál es la fecha más reciente en la cual hemos contactado a cada uno de los clientes.
Podemos resolver este problema de dos maneras: con fórmulas matriciales y con tablas dinámicas.

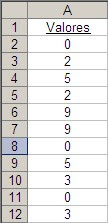
Supongamos esta tabla

Solución con fórmulas matriciales.

Empezamos creando una lista donde en la primer columna ponemos los nombres de los clientes



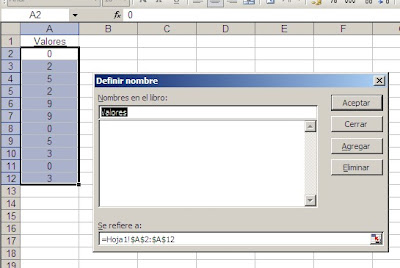
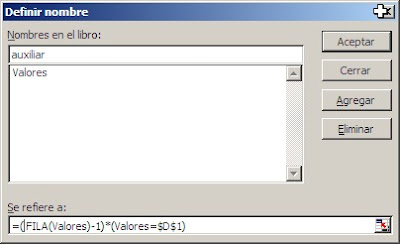
El segundo paso consiste en definir dos nombres: clientes que contiene el rango A2:A15 y fechas que contiene el rango B2:B15

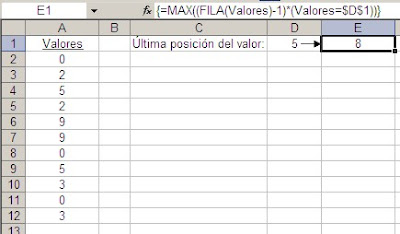
En la celda D2 ponemos esta formula matricial

=MAX((clientes=D2)*fechas)

Como toda fórmula matricial la introducimos apretando simultáneamente Ctrl+Mayúsculas+Enter. Ahora copiamos la fórmula a las restantes celdas del rango



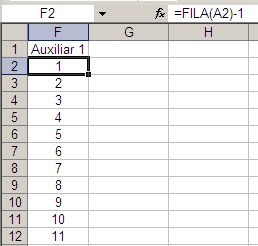
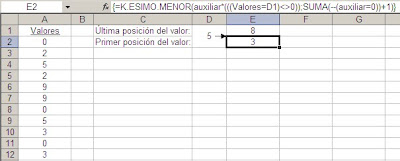
Para explicar como funciona esta fórmula matricial, veamos una solución que usaría columnas auxiliares.



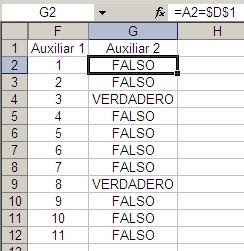
En la primer columna auxiliar comparamos si el cliente de la fila coincide con el cliente que estamos buscando (en nuestro caso Cliente 1).



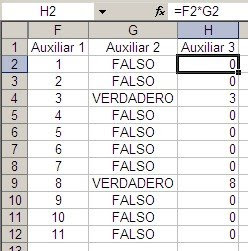
En la segunda columna auxiliar simplemente multiplicamos la columna de las fechas por la primer columna auxiliar. Dado que Excel interpreta VERDADERO como el valor 1 y FALSO como 0, obtenemos fechas sólo para el cliente 1. Ahora es evidente que la fórmula =MAX(D2:D15) nos dará la última fecha del Cliente 1.
Al usar nuestra fórmula matricial hacemos lo mismo pero evaluando cada uno de los clientes de acuerdo a la fila en la tabla de resultados.

Esta solución tiene dos inconvenientes:
1 - si se trata de una hoja con una gran cantidad de datos, el recalculado de la hoja puede ser muy lento.
2 - Cada vez que agreguemos un cliente a nuestra base de datos, tendremos que modificar la tabla de resultados agregando el cliente y copiando la fórmula.

Estos inconveniente se pueden superar usando tablas dinámicas en lugar de fórmulas matriciales.

Solución con tablas dinámicas.

Seleccionamos la celda A1 (o cualquier celda de la lista) y creamos una tabla dinámica



Arrastramos el campo Clientes al área de filas y el campo Fechas al área de datos



Activamos el menú de configuración de campo para el área de datos y hacemos estos cambios:

# - elegimos resumir por Máx



# elegimos el formato de fecha para los valores



Como podemos ver obtenemos el mismo resultado como con las fórmulas matriciales



Por supuesto, la fila Total General no tiene ningún sentido, por lo cual quitamos la señal de la opción Totales generales de columnas en el menú Opciones de tabal dinámica.



Esta solución es más eficiente que la anterior. Podemos usar rangos dinámicos para que las nuevas entradas sean procesadas automáticamente al actualizar la tabla dinámica.

El cuaderno con el ejemplo se puede descargar aquí

Technorati Tags: MS Excel

Gráficos de distribución normal (Gauss) con Excel.

Hace unos días me preguntaba un lector cómo se puede crear con Excel un gráfico tipo campana de Gauss para representar un informe de desviaciones estándar.
Empecemos por citar a Wikipedia:

…la llamada distribución normal…[se utiliza] como modelo en multitud de variables (peso, altura, calificaciones...), en cuya distribución los valores más usuales se agrupan en torno a uno central y los valores extremos son escasos.

La representación gráfica de la distribución normal se ve así:



Lo que nos dice este gráfico es que en la distribución normal los miembros de la muestra se concentran alrededor del promedio y son más escasos a medida que nos vamos a los extremos. En la distribución normal cerca del 68% de los miembros de la muestra se ubican a en el área definida por un desvío estándar en cada sentido

En esta nota veremos cómo crear gráficos de distribuciones normales con las herramientas que nos provee Excel.
Para definir una distribución normal necesitamos una colección de datos de los cuales calcularemos el promedio y el desvío estándar. Por ejemplo, para crear este gráfico



hemos definido el desvío estándar en la celda B1 (1) y el promedio en la celda B2 (0), en el rango A5:A29 hemos puesto una serie de datos que va de -3 a +3, es decir de menos tres desvíos estándar a más tres desvíos estándar



Los valores en el rango B5:B29 están calculados con la fórmula

=DISTR.NORM(A5;Media;DesvEst;FALSO)

donde Media  DesvEst es el nombre de la celda B1 y Media el de la celda B2. Los valores del rango A5:A29 son el resultado de tomar 3 desvíos estándar de “izquierda a derecha” (-3 x DesvEst = -3).
También podemos representar la distribución normal con un gráfico de área



En resumen, para crear un gráfico de distribución normal necesitamos la serie que de datos que queremos analizar, obviamente, la función PROMEDIO, la función DESVEST para calcular el desvío estándar y la función DISTR.NORM para calcular la distribución normal para la media y desviación estándar de cada dato de la serie.


Para ampliar un poco más la explicación pongamos por ejemplo una serie de 500 datos.



Los datos los hemos puesto en el rango Datos (A2:A501); en E1 hemos calculado el promedio de los datos y en E2 el desvío estándar.
En el rango C5:C25 creamos una serie de grupos, es decir, intervalos de frecuencia de los datos. Para calcular cuántos datos caen en cada grupo usamos la función FRECUENCIA

={FRECUENCIA(datos;grupos)}

Esta es una función matricial y la introducimos pulsando Ctrl+Mayúsculas +Enter luego de haber seleccionado todo el rango.
Finalmente calculamos al distribución normal con

=DISTR.NORM(C5;$E$1;$E$2;FALSO)

en el rango E5:E25

Con estos datos podemos crear un histograma (también pueden consultar esta nota) y en el mismo gráfico agregar la distribución normal de los datos con un gráfico de línea (usando un eje secundario)




Este gráfico nos permite comparar el histograma creado a partir de los datos con la distribución normal teórica.

El archivo de este ejemplo se puede descargar aquí.



Technorati Tags: MS Excel

Calcular la posición de un elemento en un rango de Excel.

Un lector me consultaba cómo calcular la posición del último 5 en esta lista



Podemos ver que el último 5 ocupa el octavo lugar en la lista (o vector) y que se encuentra en la fila 9 de la hoja. En esta nota veremos cómo encontrar dinámicamente la última posición de cualquier elemento de la lista.

Por comodidad empezamos por definir un nombre que contenga el rango de la lista




En la celda D1 ponemos el número de la lista cuya última posición buscamos (esto nos permitirá usar nuestra fórmula en forma dinámica) y en la celda E1 ponemos esta fórmula matricial

=MAX((FILA(Valores)-1)*(Valores=$D$1))

Como toda fórmula matricial debe ser ingresada a la celda apretando simultáneamente Ctrl+Mayúscula+Enter



Podemos explicar esta fórmula mostrando la alternativa de usar columnas auxiliares. En ese caso empezamos por construir una columna auxiliar para calcular la posición del elemento en la lista. Esto lo hacemos calculando la fila de la celda con la función FILA y restando del resultado el número de filas desde la fila 1 hasta la primer fila de la lista (en nuestro caso 1)



Nuestra segunda columna auxiliar calculará si el valor de la celda coincide con el valor que estamos buscando



Como vemos el número 5 ocupa el tercer y el octavo lugar en la lista.

Nuestra tercer columna auxiliar consiste en multiplica Auxiliar1 por Auxiliar 2



Ahora es fácil ver que la fórmula =MAX(H2:H12) da como resultado 8, que es la posición del último 5 en la lista. Todo esto lo hemos comprimido en una única fórmula matricial, como mostramos más arriba.

Ahora, envalentonados con nuestro dominio de Excel, queremos calcular la posición del primer 5. No podemos usar la función MIN ya que en el vector de la fórmula matricial siempre habrá algún 0 y por eso siempre nos dará la posición 0 como resultado.
Aquí echamos mano a la función K.ESIMO.MENOR. Esta función da como resultado el k-ésimo menor valor de un conjunto de datos. En nuestro caso queremos encontrar el menor valor de la matriz (FILA(Valores)-1)*(Valores=$D$1) (es decir, Auxiliar 3) sin tomar en cuenta los valores 0.
Para esto necesitamos calcular cuantos 0 hay en el vector. La idea más obvia es usar CONTAR.SI, pero esta función tiene un problema: no se puede usar en fórmulas matriciales. En lugar de CONTAR.SI usaremos SUMA:

=K.ESIMO.MENOR(( FILA(Valores)-1)*(Valores=Hoja1!$D$1)*(((Valores=D1)<>0));SUMA(--(FILA(Valores)*(Valores=D1)=0))+1)

Recordemos que ésta es una fórmula matricial (Ctrl+Mayúsculas+Enter)

Para simplificar nuestra fórmula definimos el nombre "auxiliar" que contendrá la matriz creada por la expresión

auxiliar =( FILA(Valores)-1)*(Valores=Hoja1!$D$1)



Ahora podemos construir la fórmula en forma más legible:

=K.ESIMO.MENOR(auxiliar*(((Valores=D1)<>0));SUMA(--(auxiliar=0))+1)




El archivo con el ejemplo se puede descargar aquí

Technorati Tags: MS Excel