Excel's FORECAST function post in English
En la primera entrada de este blog, había explicado como encontrar la intersección de dos líneas en un gráfico de Excel. Para hacer esto utilizamos la opción "línea de tendencia" (trendline) y el SOLVER.
Con Excel podemos, dada una tabla de valores, predecir un valor futuro a partir de valores existentes utilizando la función PRONOSTICO (FORECAST) (apretar el enlace para descargar el archivo).
La descripción de la función PRONOSTICO de acuerdo a la ayuda online de MS Excel es la siguiente:
Calcula o pronostica un valor futuro a través de los valores existentes. La predicción del valor es un valor y teniendo en cuenta un valor x. Los valores conocidos son valores x y valores y existentes, y el nuevo valor se pronostica utilizando regresión lineal. Esta función se puede utilizar para realizar previsiones de ventas, establecer requisitos de inventario o tendencias de los consumidores.
La sintaxis es: PRONOSTICO(x;conocido_y;conocido_x), donde
X es el punto de datos cuyo valor desea predecir.
Conocido_y es la matriz o rango de datos dependientes.
Conocido_x es la matriz o rango de datos independientes.
En nuestro ejemplo tenemos una tabla que muestra cantidades vendidas a cada nivel de precios:
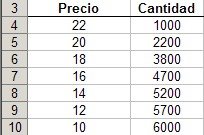
Los valores de "precios" corresponden al argumento Conocido_X; los valores de "cantidad" corresponden a Conocido_y.
Para calcular la cantidad prevista si el precio fuera 8, aplicamos la siguiente fórmula: =PRONOSTICO(A11,B4:B10,A4:A10)
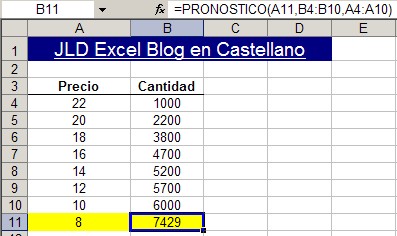
También podemos usar la técnica sugerida en mi primer entrada, averiguando la ecuación de la línea de tendencia (trendline) en el gráfico, y luego aplicándola como fórmula en la hoja de cálculo.
Para ver la ecuación de la línea de tendencia, creamos el gráfico a partir de la tabla y luego abrimos el menú "agregar línea de tendencia", apretando el botón derecho del mouse sobre la curva del gráfico.
Una vez que aparece la línea de tendencia, abrimos el menú "formato línea de tendencia":
- en la pestaña "tipo" elegimos "lineal"
- en la pestaña "opciones", chequeamos "presentar ecuación en el gráfico"
Finalmente insertamos la función de la línea de tendencia como formula en una celda de la hoja de cálculo.
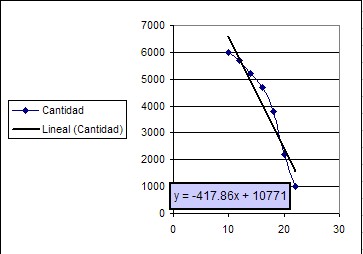
En nuestro ejemplo en anotamos =-417.86*B16+10771 en la celda B17), donde la celda B16 contiene el valor para el cual queremos pronosticar el resultado.
Categorías: Funciones&Formulas_
Technorati Tags: Función PRONOSTICO, FORECAST Function
En una las primeras entradas que publiqué en este blog, di una explicación general sobre las fórmulas matriciales (array formulas) en Excel.
Esa entrada se limitaba a mostrar un aspecto del uso de las funciones matriciales. El objetivo de esta nota es ampliar la explicación sobre esta importante herramienta de Excel.
Una matriz es un conjunto ordenado de elementos. En términos de Excel, una matriz puede ser un rango contenido en una columna (o fila), que es una matriz unidimensional, o en un rango rectangular, lo que la convierte en una matriz bidimensional.
En el ejemplo de la explicación general sobre fórmulas matriciales, una matriz era el rango A2:A12 la otra el rango B2:B12. En ese ejemplo usamos la fórmula matricial para calcular un promedio ponderado. Este es uno de los usos posibles de las funciones matriciales, que llamaremos "unicelular", ya que le resultado de la fórmula aparece en una sola celda.
Las funciones matriciales de Excel también pueden usarse para obtener el resultado de un cálculo en varias celdas simultáneamente, lo que llamaremos fórmulas matriciales "multicelulares". Por ejemplo, podemos rescribir el ejemplo de la nota anterior de la siguiente manera:
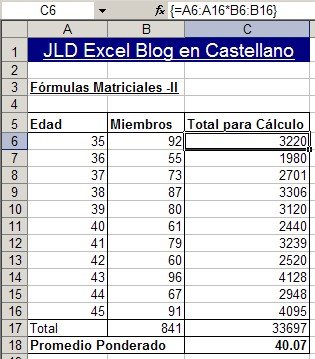
Como pueden ver en el ejemplo (descargar el 
ejemplo de fórmulas y constantes matriciales aquí), la fórmula es la misma a lo largo del rango C6:C16, pero el resultado en cada celda es el producto de las celdas de la fila correspondiente.
Este tipo de fórmulas matriciales no parece tener ninguna ventaja sobre las fórmulas matriciales "unicelulares". Tal vez una de las ventajas sea que Excel no permite borrar parcialmente estas fórmulas, y por lo tanto es un buen método de proteger las fórmulas en las hojas de cálculo.
Un aspecto más interesante es la posibilidad de crear matrices constantes en Excel. Al crear una matriz de este tipo, los datos son almacenados en la memoria del computador, y no en rangos de la hoja de cálculo.
Para crear una matriz de constantes, escribimos los miembros de la matriz entre signos "{" y "}", separados por ";" (matriz horizontal) o por "\" (matriz vertical). Por ejemplo: {1;2;3;4;5} genera una matriz horizontal de cinco miembros
Aclaración: la ayuda de Excel en español sostiene que para generar una matriz orientada horizontalmente habrá que separar los miembros con comas; para generar una matriz vertical, la separación será hecha con punto y coma ";". En la versión de Excel de este ejemplo (XL 2002), los separadores al usar el lenguaje Español, son los indicados más arriba. Al abrir el mismo cuaderno con el lenguaje Inglés, Excel reemplaza los separadores por ";" y "\".
Una forma más cómoda de trabajar con matrices de constantes es asociarlas a un nombre, como he mostrado en mi entrada sobre uso de nombres en MS Excel. Por ejemplo, si creamos el nombre "Semana" que contenga una matriz con los días de la semana {"lunes","martes","miércoles","jueves", "viernes","sábado","domingo"}. Estas matrices pueden luego ser empleadas en fórmulas, tanto matriciales como fórmulas comunes.
Por ejemplo, si usamos el nombre "semana" que acabamos de definir en esta fórmula =INDEX(semana,2), obtenemos como resultado "martes".
Matrices, matrices nominadas y fórmulas matriciales, son elementos indispensables para convertirse en usuario avanzado de Excel.
Categorías: Formulas Matriciales_
Technorati Tags: Fórmulas Matriciales, Constantes Matriciales
En notas anteriores vimos una explicación básica de la función SUMAPRODUCTO y como utilizar SUMAPRODUCTO para contar condicional con varias condiciones.
El uso de SUMAPRODUCTO supone que se cumplen dos condiciones obligatorias:
1 – Los rangos son del mismo tamaño, es decir tienen la misma cantidad de miembros
2 – Los rangos tienen la misma orientación, filas o columnas.
A veces sucede que una de las matrices es un rango en una columna y otra matriz es un rango en una fila.
Para sobreponerse a este problema, sin tener que rehacer las hojas de cálculo, podemos utilizar la función TRANSPONER.
La definición de la función TRANSPONER en la ayuda de Excel es la siguiente:
Devuelve un rango de celdas vertical como un rango horizontal o viceversa.
TRANSPONER debe introducirse como una fórmula matricial en un rango que tenga el
mismo número de filas y columnas, respectivamente, que el número de columnas y
filas en una matriz. Utilice TRANSPONER para cambiar la orientación vertical y
horizontal de una matriz en una hoja de cálculo.
Es importante notar que se trata de una función matricial (array function).
Veamos el uso de TRANSPONER con SUMAPRODUCTO con un ejemplo (apretar el link para decargar el cuaderno)
Supongamos que tenemos esta tabla en una hoja de cálculos
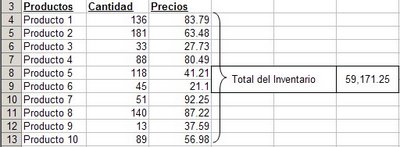Aquí el cálculo del total del inventario es sencillo, ya que las dos matrices (cantidad y precios) están orientadas en el mismo sentido
=SUMAPRODUCTO(B4:B13,C4:C13)
Pero supongamos que la matriz de Precios esté en un rango en una fila (en nuestro ejemplo en el rango A17:K17). En este caso usamos la función TRANSPONER para convertir la matriz de precios de fila a columna. La fórmula es
={SUMAPRODUCTO(B4:B13,TRANSPONER(B17:K17))}
Debemos prestar atención a los símbolos "{" y "}" al principio y al final de la fórmula. Ya que TRANSPONER es una función matricial, SUMAPRODUCTO debe ser anotada como tal, es decir apretando Ctrl+Shift junto con Enter.
Ya que hemos convertido a SUMAPRODUCTO en una función matricial, podemos utilizar la función SUMA, en forma matricial, de la siguiente manera:
={SUMA((B4:B13)*TRANSPONER(B17:K17))}
Categorías: Funciones&Formulas_, Formulas Matriciales_
Technorati Tags: SUMAPRODUCTO, TRANSPONER
