Ranking con Excel y con Power Query

Un docente me consulta sobre como ordenar una lista de alumnos de acuerdo a sus calificaciones. El problema del docente era cómo determinar la posición (ranking) de cada alumno en caso de empate (es decir, dos o más alumnos con la misma calificación).

Según Wikipedia hay cinco métodos de calcular la posición de un elemento en una lista (ranking)

• Ordinal simple (1,2,3,4): cada elemento recibe un número de clasificación secuencial sin tomar en cuenta "empates".
• Competencia estándar (1,2,2,4): los elementos que "empatan" reciben el mismo número de clasificación, y luego se deja un hueco en los números de clasificación.
• Competencia modificada (1,3,3,4): la clasificación se hace dejando los huecos en los números de clasificación antes de los conjuntos de elementos de igual rango (en lugar de después de ellos como en la clasificación estándar de la competencia).
• Clasificación Densa (1,2,2,3): los artículos que se "empatan" reciben el mismo número de clasificación, y los siguientes artículos reciben el número de clasificación inmediatamente posterior. 
• Clasificación fraccionada (1,2.5,2.5,4): los artículos que "empatan" reciben el mismo número de clasificación, que es la media de lo que tendrían en las clasificaciones ordinales. 

En un próximo post volveré sobre el tema de los métodos de ranking. En este post me centraré en el método ordinal simple y algunas variaciones. Digamos que ésta sea la lista de alumnos:

En Excel "Clásico" contamos con tres funciones para calcular ranking: JERARQUIA(), JERARQUIA.EQV() y JERARQUIA.MEDIA
Si aplicamos esta funciones a la lista de alumnos obtendremos:

Como podemos ver JERARQUIA.EQV calcula según el método de competencia estándar y JERARQUIA.MEDIA según clasificación fraccionada.

Nuestro buen docente necesita una clasificación ordinal, lo que se puede hacer sencillamente ordenando la lista de mayor a menor según las calificaciones. Pero ésto deja abierto el problema del "desempate". Digamos que en caso de empate, clasificamos por orden alfabético. El problema con Excel "Clásico" es que al ordenar por una columna "desordenamos" las otras. Lo mismo ocurre si queremos aplicar un criterio de género, por ejemplo, preferencia a las alumnas o asignando un número aleatorio a los alumnos.

Todo esto lo podemos superar usando Power Query.

Clasificación ordinal con Power Query.

Clasificación ordinal sencilla.
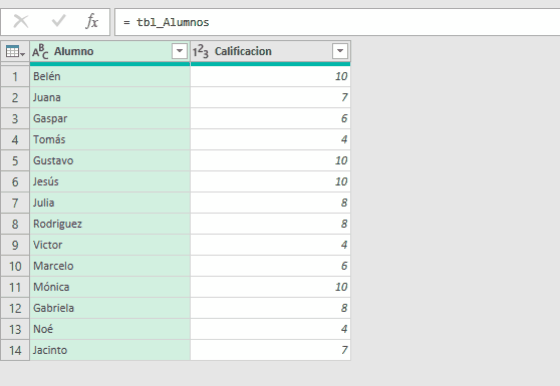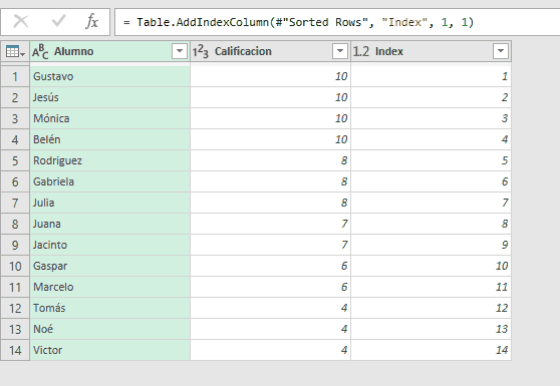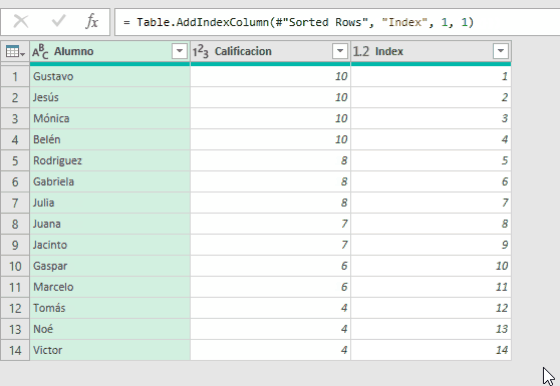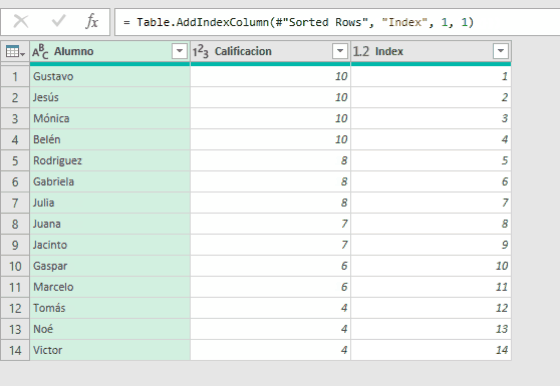
Sencillamente creamos la consulta, ordenamos la tabla de mayor a menor según [Calificacion] y agregamos una columna personalizada con Índice

Clasificación ordinal con desempate alfabético.
Supongamos que en caso de empate el orden se decide alfabéticamente  (de A a Z). Lo que no podíamos hacer con Excel Clásico lo hacemos con Power Query. Creamos la consulta, ordenamos por [Calificacion] y luego por [Alumno]. Finalmente agregamos una columna Indice

Clasificación ordinal con desempate aleatorio.
Aparentemente la solución es sencilla: crear una columna de números aleatorios con la función Number.Random y luego ordenar por la columna de las calificaciones y la de números aleatorios. Pero al hacerlo nos espera una desagradable sorpresa: todas las filas muestran el mismo número

En esta discusión  en el foro TechNet se sugieren varias soluciones. La única que me ha dado el resultado deseado es agregando una columna de índice (empezando en 0) y usando la función List.Random en lugar de Number.Random. El código de la consulta es

 let  
   Origen = Excel.CurrentWorkbook(){[Name="tbl_Alumnos"]}[Content],  
   #"Tipo cambiado" = Table.TransformColumnTypes(Origen,{{"Alumno", type text}, {"Calificacion", Int64.Type}}),  
   #"Índice agregado" = Table.AddIndexColumn(#"Tipo cambiado", "Índice", 0, 1),  
   #"Personalizada agregada" = Table.AddColumn(#"Índice agregado", "Aleatorio", each List.Random(Table.RowCount(#"Índice agregado")){[Índice]}),  
   #"Filas ordenadas" = Table.Sort(#"Personalizada agregada",{{"Calificacion", Order.Descending}, {"Aleatorio", Order.Ascending}}),  
   #"Índice agregado1" = Table.AddIndexColumn(#"Filas ordenadas", "Índice.1", 1, 1),  
   #"Columnas quitadas" = Table.RemoveColumns(#"Índice agregado1",{"Índice"})  
 in  
   #"Columnas quitadas"  

Descargamos la consulta a una hoja de Excel y obtenemos

Podemos también eliminar la columna [Aleatorio] que he dejado solamente a los efectos del ejercicio.